안녕하십니까 여러분들을 '발전' 시켜줄 핵발전소입니다.
레버리지 투자를 장기적으로 해선 안된다는 말 많이 들어보셨을 겁니다.
과연 장기투자를 하면 계좌가 녹아버릴까요?

이런 내용을 다룬 것은 유튜브에서 쉽게 찾아볼 수 있습니다.
ETF 자산이 10% 내리고 10% 오르면 손실이 난다는 이론인데요.
100만 원이 -> 90만 원 (10 % 하락 시)
90만 원이 -> 99만 원 (10 % 상승 시) 기초자산 1만 원이 증발했다는 이론 Vol drag현상인데요.
레버리지를 사용했을 때 더 큰 손실을 안겨준다는 내용입니다.
100만 원이 -> 80만 원 (20% 하락 시)
80만 원이 -> 96만 원 (20% 상승 시) 기초자산 4만 원 증발
과연 맞는 말일까요?
손실이 과속화되는 것은 맞지만.
그럼 1 배수를 사더라도 오래 가지고 있으면 0원이 된다는 말인데.
이에 대해 설명을 해준 좋은 글을 찾게 되어서 여러분에게 전하고자 합니다.
의역, 오역 조금 있을 수 있습니다 양해 부탁드립니다.
http://www.ddnum.com/articles/leveragedETFs.php
Double-Digit Numerics - Articles - The Big Myth about Leveraged ETFs
www.ddnum.com
[For a longer and more interesting version of this article check out the paper Alpha Generation and Risk Smoothing using Managed Volatility] ->논문입니다.
레버리지 ETF의 장기적인 움직임
최근 미디어에 전파된 레버리지 ETF에 대한 큰 신화(잘못된 생각)가 있습니다.
이 글은 신화를 수정하고 그것을 일으킨 잘못된 추론을 설명합니다.
그 신화는 다음과 같습니다.
"레버리지 ETF는 장기 매수 및 보유에 적합하지 않습니다."
이 신화는 다양한 방식으로 표현됩니다. 레버리지 ETF에 대한 인터넷 글들:
매수 및 보유 투자에 적합하지 않음.
레버리지 ETF는 악화될 수 있습니다.
시간이 지남에 따라 복리가 죽을 것입니다.
레버리지 ETF가 정신이상에 휩싸입니다.
레버리지 ETF는 독성이 있습니다.
끔찍한 아이디어.
실질적으로 손실을 보장합니다.
장기적으로는 거의 손실을 입을 것입니다.
경고! : 레버리지 및 인버스 ETF는 포트폴리오를 죽입니다.
이러한 주장은 수학과 데이터로 뒷받침되지 않습니다.
이 글은 그 결함을 수정하고 주장이 거짓임을 설명합니다.
이 신화에 대해 일반적으로 주어진 설명은 변동성으로 인해 장기 수익률에서 자본이 사라진다는 것입니다.
이것이 사실이라면 비 레버리지 펀드도 변동성으로 인해 어려움을 겪기 때문에 매수 및 보유에 적합하지 않을 것입니다.
레버리지형 ETF 란?
레버리지 ETF는 매일 벤치마크 수익의 배수 수익을 약속하는 ETF로 정의된 것입니다.
예를 들어 ETF가 S&P 500 지수의 2배 수익을 약속하면 S&P 500 지수가 하루 만에 1.2 % 상승하면
ETF는 2 X 1.2% = 2.4% 상승합니다.
이 정의에 대한 중요한 점은 배수가 -3 또는 2.5와 같은 숫자일 수 있으며 배수 1을 포함할 수 있으며, 매년 반환이 아니라 매일 벤치마크에 표시된다는 것입니다. 연간 수익률을 측정해도 그렇다. 그중 1 배수는 대부분의 사람들이 이러한 ETF를 레버리지 된 ETF라고 부르지 않지만 기술적으로는 레버리지 1을 가진 ETF입니다.
신화(잘못된 생각)의 기원
일일 변동성은 레버리지 ETF의 수익률을 손상시킨다. (1 배수 ETF 포함)
(1 - x)(1 + x) = 1 - x^2
시장이 x 내려갔다가 다음날 x 올라간다고 가정해 봅시다.
예를 들어 x = 0.05 이면 시장이 5% 상승했다가 5% 하락합니다.
그 후 순이익률은 0.25% 하락하는 (1-0.05)(1+0.05) = 0.9975까지 상승하였습니다.
이건 불공평해! 시장은 5% 하락했다가 상승했지만 레버리지 1 배수를 가진 우리 ETF는 0.25% 하락했습니다.
오우 쉣!
x^2는 항상 양수이고(제곱) 앞에 있는 기호는 음수이기 때문에 이 하락이 항상 발생합니다.
그래서 시장이 변동성이 있을 때마다 우리는 돈을 잃습니다.
우리는 이것을 volatility drag (변동성 드래그)라고 합니다.
이러한 속설은 시간이 충분할 경우 레버리지 ETF를 0으로 끌어내릴 것이라는 믿음에서 비롯되었습니다.
그러나 우리는 레버리지 1 배수가 volatility drag 효과가 있음에도 불구하고 레버리지 1 배수 (즉 레버리지 없음)
ETF는 영구적으로 보유해도 안전하다는 것을 알고 있습니다.
레버리지 1 배수가 안전하다면 레버리지 1.01 배수는 안전할까요?
1.1 배수는 안전할까요?
2 배수라는 수치는 수학적으로 특별한 점이 존재하는 것일까요?
안전과 위험의 선은 어떻게 규정해야 할까요?
어쩌면 2배 정도는 안전할 겁니다.
레버리지 2 배수를 사용하는 ETF가 영구적으로 보유하기에 적합하지 않은 이유는 무엇입니까?
물론 이유가 있을 수 있지만 volatility drag효과 때문인 것은 아닙니다.
이 신화의 오류는 쉽게 증명된다.
아래 차트는 1885년 2월부터 124년 치 미국 일일 지수 가격을 보여줍니다.
이 지수의 구성은 Schwert(1990)에 기술되어 있으며, 사용된 지수는 자본 지수(재투자된 배당금은 없음)입니다.
Yahoo.com의 S&P 500 데이터는 2009년까지 데이터를 가져오는 데 사용되었습니다.
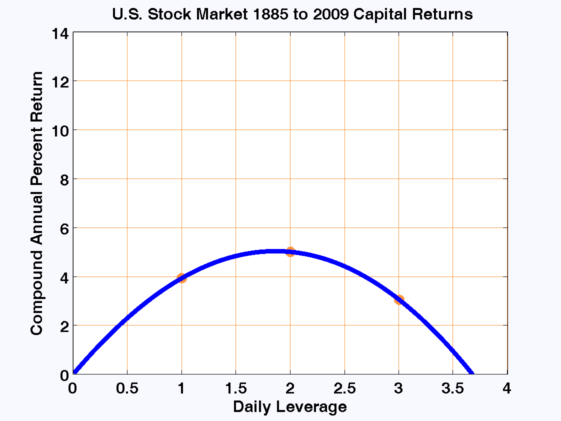
주황색 점은 인기 있는 레버리지 비율 1, 2, 3을 보여주고, 참고를 위해 4배도 있습니다.
레버리지를 0 배수에서 1 배수로 증가시키면 예상대로 연간 수익률이 증가한다는 것을 알 수 있습니다.
그러나 신화 전파자들이 말하는 것과는 반대로 레버리지를 더 높이면 여전히 수익이 증가합니다.
레버리지 값 1 배수에서 어떤 특별한 의미도 찾을 수 없습니다.
1 배수에서 갑자기 수익률이 하락할 어떤 특별한 수학적 근거가 없는 셈이죠.
그러니 신화는 잘못되었습니다.
레버리지 ETF는 장기적으로 보유할 수 있습니다.(124년이라면 충분히 장기투자)
물론 레버리지 값이 약 2에 도달하면 수익이 감소한다는 것을 알 수 있습니다.
그것이 volatility drag효과입니다.
이런 주장의 논리적 오류가 생긴 이유는, 레버리지 ETF의 수익률을 결정하는 근거가 벤치마크의 수익률과 벤치마크의 변동성 두 가지만 이라는 점 때문입니다.
벤치 마크가 긍정적인 수익을 내면(장기적 우상향) 레버리지에 노출된 것이 수익이 좋으며
volatility drag 효과를 뛰어넘습니다.
물론 수익은 레버리지의 배수로 결정되고, volatility drag 또한 레버리지의 배수이므로
volatility drag는 레버리지가 높아질수록 얻은 추가 레버리지 리턴을 압도합니다.
그래서 활용할 수 있는 레버리지의 양에는 한계가 있습니다.
-> 풀이하자면 장기적 우상향 하는 S&P 500 같은 지수에서는 적절한 레버리지 노출은 volatility drag의 손실보다 큰 효과를 내서 추가 수익을 얻을 수 있습니다. 그러나 배수가 커질수록 volatility drag 효과도 커져 4 배수에 가까워지면 수익률 잠식이 일어나게 됩니다.
ETF 장기 수익률 공식
레버리지 ETF의 장기 수익률은 단지 벤치마크 수익률 및 변동성만으로 설명될 수 없습니다.
또한 벤치 마크의 왜도( Skewness ) 및 첨도 ( kurtosis )를 포함하는 항을 포함합니다.
->논문에서 자세히 보실 수 있습니다.
벤치 마크 수익률이 가우스이거나 Ito의 기본형을 사용하여 파생된 공식처럼 수익률이 연속적이라고 가정하지 않습니다.
그러나 세계 주식 시장의 3 이하의 낮은 수준의 레버리지의 경우 다음 공식으로 대략적으로 정의할 수 있습니다.
R = kμ - ½k^2σ^2/(1 + kμ)
여기서 R은 ETF의 일간 기하 수익률(일간 복리 수익률), k는 ETF 레버리지 배수,
μ는 벤치마크의 평균 일일 수익률, σ는 벤치마크의 일일 수익률(즉, 표준 편차)입니다.
R 은 ETF의 장기 매수 및 보유 수익을 계산하는 데 사용됩니다. 공식을 통해 변동성이 0이면 R = kμ가 나와 ETF의 수익률이 기준치 수익의 k배임을 알 수 있습니다.
½k^2σ^2/(1 + kμ) 항은 volatility drag입니다. k^2σ^2는 항상 양수이고 (1 + kμ)는 항상 1에 가까우므로 volatility drag 도 아쉽게도 항상 양수입니다.
R은 k의 2차 함수로 제곱 항에 대한 음의 계수를 갖습니다.
그것은 우리가 항상 위에 보이는 포물선 모양을 얻을 것이고 우리는 항상 k의 어떤 값에 대해 최댓값을 가질 것이라는 것을 의미합니다.
일부 대수에서는 최대치가 k = μ/σ^2 임을 보여줍니다.
이것은 최적의 레버리지(recession)를 결정하는 수익 / 변동성 트레이드오프를 명확히 보여줍니다.
이 공식(실제로 Skewness와 kurtosis를 포함한 더 정확한 버전)은 전체 논문에서 심층적으로 논의됩니다.
켈리 기준과 머튼의 포트폴리오 문제에서 적절한 형태로 나타나는 공식입니다.
최적화의 결과로 나타난 그것의 모습은 놀랄 일이 아닙니다.
아래 표는 R 대 μ 및 σ를 표시합니다.
대부분의 사람들이 연간 수익률에 대해 생각하는 데 익숙해졌기 때문에 세 가지 수량은 모두 연간화 되었지만
여전히 일일 수량입니다.
차트는 이해하기 어려울 수 있습니다.
그러나 중요한 점은 일별 변동성을 증가시키는 방향으로 차트에서
수평으로 오른쪽으로 이동하면 해당 일별 복귀의 경우 R이 더 파란색이 됩니다.
즉, R이 감소합니다.
volatility drag 효과입니다.
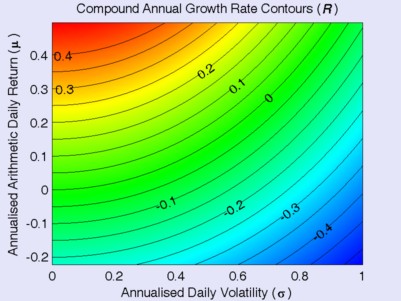
이 차트의 이점은 모든 레버리지 k에 대해 차트에 레버리지 ETF를 동시에 표시할 수 있다는 것입니다.
다음 섹션의 차트에 있는 숫자 1 ~ 4는 레버리지 1 ~ 4의 포인트가 어디에 있는지 보여줍니다.
일일 변동성과 일일 수익은 모두 k에 따라 선형 적으로 증가하므로 다양한 레버리지가 차트에 직선을 그립니다.
R 윤곽이 곡선 이기 때문에 직선은 곡선을 교차해야 합니다.
따라서 모든 라인의 최적 값은 R입니다.
즉, 장기 수익이 극대화되는 최적의 레버리지가 있습니다.
그리고 그 최적 레버리지는 거의 항상 1 배수보다 큽니다.
최적 레버리지는 얼마일까?
다른 시장과 기간을 살펴보겠습니다.



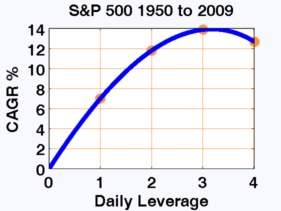
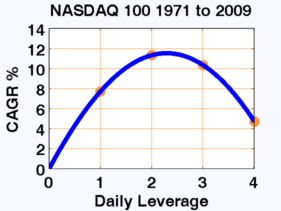
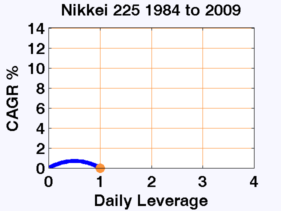
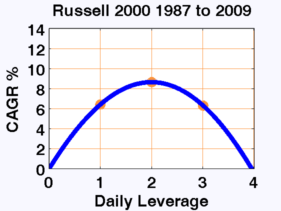

이러한 시장 중 일부(그리고 다른 시장들은 명확성을 위해 제외)를 우리의 등고 선도에 플로팅 하는 것은
R이 레버리지에 따라 어떻게 변화하는지를 보여주며 우리가 모든 시장을 한 번에 볼 수 있게 해 줍니다.
레버리지에 따라 R이 어떻게 바뀌는지 볼 수 있습니다.

패턴은 아주 분명합니다. 니케이 225를 제외하고 다양한 기간 (대부분 지난 20 년 정도)의 다양한 시장에서 최적의 레버리지는 약 2입니다.
예외는 Nikkei 225입니다. 최적의 레버리지는 약 0.5 배수입니다.
특이한 경우인 것이 이 시장에 레버리지 1배 수로 투자했다면 누적수익률은 0인데 반하여, 절반은 현금으로 쥐고 제로금리로 유지하면 복리 수익률이 0.7% 가 됩니다.
이 점은 모순되는 부분이 있습니다. 전체 논문에서 자세히 논의됩니다.
레버리지 ETF를 장기간 보유하지 않는 이유가 있다면?
장기적으로는 레버리지 ETF를 보유하지 못하는 이유가 있을 수 있지만 그것은 volatility drag와 무관합니다.
유력한 것은 수수료 때문입니다.
레버리지 배수가 1 배수 이상인 ETF는 대부분 연간 약 1%의 수수료를 부과합니다.
이렇게 되면 ETF에 "fee drag(수수료 드래그)"가 부과됩니다.
또한 레버리지 ETF는 추적 오류로 인해 어려움을 겪고 있습니다.
그들은 매일 그들의 목표수익률을 정확히 맞추지는 못합니다.
몇 개의 활용된 ETF를 연구한 결과 추적 오류가 이 문서의 범위를 벗어나는 복잡한 오류라는 것이 관찰되었습니다.
예를 들어, 오류는 연속적으로 연관되어 있으며, 이는 ETF가 어느 날 마크에 약간 모자라면 향후 1일 또는 2일 동안 마크를 초과하는 경향이 있음을 의미합니다.
일반적으로 추적 오류는 ETF에 추가 변동성을 추가하고 그 결과로 인한 volatility drag가 발생합니다.
그러나 연속적인 상관관계와 상대적으로 작은 드래그 크기 때문에 수수료에 비해 수익에 미치는 효과는 작습니다.
그래서 이 글의 추적 오류는 무시됩니다.
일부에서는 volatility drag를 추적 오류라고 합니다.
volatility drag는 ETF 설계의 수학적 결과이며 결코 오류가 아닙니다.
연간 0.95%의 수수료(최근 레버리지 ETF의 대표적인 수수료)를 사용하여 1885년부터 데이터의 장기 성과를
재계산하면 수수료 전후 수익을 보여주는 다음 차트가 제공됩니다.
수수료는 레버리지의 모든 값에 대해 연간 수익률에서 0.95%를 차감합니다.

레버리지 수익 = 2 ETF가 수수료 없는 레버리지 = 1 ETF로 축소되었습니다.
따라서 레버리지의 모든 이점은 상실되었습니다.
하지만 더 짧은 기간 동안 다른 시장에서는 수수료가 그렇게 파괴적이지 않습니다.
(124년간 수수료 지불해야 1 배수와 수익 같아짐 / 1 배수 ETF도 수수료 존재함)
최적의 레버리지는 2 배수 정도이며, 심지어 2배의 ETF 수수료가 수십 년에 걸쳐 기준치를 초과한 후에도 그렇습니다.
아래의 S&P 500을 예로 들 수 있습니다.

추적 오류에 대한 하나의 가능한 모델에 따라 아래 차트입니다.
이 모델은 연속적인 상관관계가 없다고 가정하므로 추적 오류가 수익에 미치는 영향을 과대평가할 수 있습니다.
결과는 추적 오류가 미치는 영향이 미미할 수 있음을 시사합니다.

결론
시장이 volatility drag을 극복하기에 충분한 수익률을 보인다면 레버리지 ETF는 장기간 보유될 수 있다.
보통 장기적으로 우상향 하니까요.
최근 대부분의 시장에서 최적의 레버리지 범위는 약 2 배수입니다.
일부 시장과 시대에는 최대 3배 수도 효과가 유지되었습니다.
하지만 어떤 시장도 4 배수의 레버리지는 효과가 없습니다.
Myth busted! = 신화는 깨졌다!
평상시 주의할 점
이 글의 조사 결과에도 불구하고 레버리지에 대한 위험성은 존재합니다.
상승하는 시장에서 레버리지가 1 배수보다 크다면 수익이 증가합니다.
하락하는 시장에서 레버리지는 손실을 증가시킵니다. 어떤 시장에서든 레버리지가 1 배수 이상이면 변동성이 증가합니다.
레버리지 ETF는 시장이 하루 만에 엄청난 폭으로 하락하면 0으로 떨어질 수 있습니다.
즉 모든 돈을 잃을 수 있습니다.
이 글은 최적의 레버리지가 약 2 배수라는 것을 증명하지 못했습니다.
과거에 2 배수가 좋았다는 것을 증명했을 뿐.
미래는 다를 수 있습니다.
인버스는 추천하지 않습니다. 장기적으로 패배할 수밖에 없습니다.
시장이 장기적으로 우상향 하기 때문입니다.
성공적인 투자 하시길 기원합니다.
'금융 재테크 정보 > 주식' 카테고리의 다른 글
| 레버리지 ETF 장기 투자의 모든 것 (TQQQ에 미친자) (0) | 2026.02.04 |
|---|---|
| 미국주식 위험대비 방법 - FRED 부도위험과 주식의 Beta 조절 (7) | 2026.02.04 |
| 코스피 5000시대 앞으로 주의할 신호는? - 오건영 단장 (0) | 2026.02.03 |
| 부자가 되고싶다면 배당주 사지마라 (3) | 2025.03.31 |
| 24년 미국주식 양도소득세 - 12월 27일까지 250만원 공제 찬스 (6) | 2024.12.12 |